メニューに戻る

05:31 にページが自動更新されます。

十分発達したNS方程式の離散化

学籍番号
氏　　名
図のように鉛直方向から角度θ傾いた十分広い平板上を動粘度\(\nu \)の液体が重力\(g\)によって下向きに流れており，
流れが十分発達して液膜の厚さは\(h\)であった．この液膜内の速度分布\(u(y)\)のNS方程式は次式で簡素化できる．
\( \Large \frac{d^2 u}{d y^2} \normalsize = - \Large \frac{g}{\nu } \normalsize \cos{\theta} \cdot\cdot\cdot\cdot\cdot (1)\)
なお，動粘性係数\(\nu=\Large\frac{\mu}{\rho}\)である．
上式を差分法により離散化して数値的に解くことにする．流れを解く領域 \(\left( 0 \le y \le h \right)\) の分割数 n とする．
(A) 分割幅\(\Delta y\)はどのように表せるか？ \(\Delta y = \) ()
(B) 分割点を\( y_i, i = 0,1, \cdot\cdot\cdot ,n\)と表せば,\( y_i \)はどのように表せるか？ \(y_i = \) ()
(C) 分割点の速度\( u(y_i), i = 0, 1, \cdot\cdot\cdot ,n\)を\( u_i, i = 0,1, \cdot\cdot\cdot ,n\)と表す．
領域内部の分割点\( i = 1, \cdot\cdot\cdot ,n-1\)の任意の \(i\) について，式(1)を離散化すると，左辺はどのように表せるか？		 \(左辺 = \) ()
(D) 式(1)の右辺に(C)の分母を掛けた項を\(A\)とおくと，\(A\)はどのように表せるか？ \(A = \) ()
(E) \( i= 2\)における離散化された式(1)はどのように表せるか？ \(A = \) ()
(F) \( y = 0\)における境界条件は\( u = 0\)であり，\( y = h\)における境界条件は？ \( \) ()
(G) \( y = h\)における一階微分\( \Large \frac{d u}{d y} \normalsize\) の差分は前進差分，中心差分，後退差分のどれを用いる？ \( \) ()
(H) (G)を離散化するとどのように表せるか？ \( \) ()
1階微分：\(\displaystyle\frac{du}{dy}\)　前進差分\(\displaystyle \frac{u(y+\Delta y)-u(y)}{\Delta y}\), 後退差分\(\displaystyle \frac{u(y)-u(y-\Delta y)}{\Delta y}\), 中心差分\(\displaystyle \frac{u(y+\Delta y)-u(y-\Delta y)}{2 \Delta y}\)
2階微分：\(\displaystyle\frac{d^2 u}{dy^2}\)　中心差分\(\displaystyle \frac{u(y+\Delta y)-2 u(y)+u(y-\Delta y)}{(\Delta y)^2}\)
傾斜平板に沿う流れ

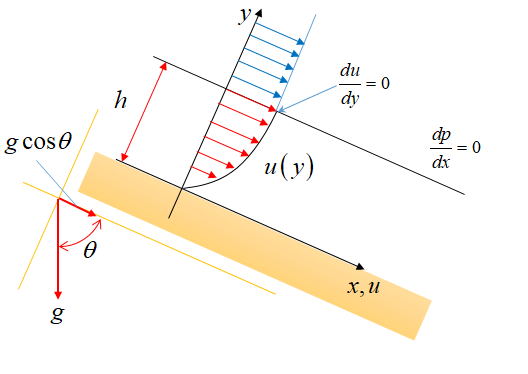
図0013 傾斜平板に沿う流れ



選択肢

(1)\(\Large \frac{u_{i+1} - 2 u_i +u_{i-1}}{(\Delta y)^2} \normalsize\) (2)\(- \Large \frac{g (\Delta y)^2}{\nu } \normalsize \cos{\theta} \) (3)\(\Large \frac{h}{n} \normalsize\)
(4)\(後退差分\) (5)\(\Large \frac{u_{n+1}-u_{n}}{\Delta y} \normalsize = 0\) (6)\(\Large \frac{u_{n}-u_{n-1}}{\Delta y} \normalsize = 0\)
(7)\(u_{3} - 2 u_2 +u_{1}\) (8)\(- \Large \frac{g }{\nu (\Delta y)^2} \normalsize \cos{\theta} \) (9)\(u_{4} - 2 u_3 +u_{2}\)
(10)\(\Large \frac{u_{n+1}-u_{n-1}}{2 \Delta y} \normalsize = 0\) (11)\(u = 0\) (12)\(y_0 + n \times \Delta y\)
(13)\(\Large \frac{d u}{d y} \normalsize = 0\) (14)\(中心差分\) (15)\(前進差分\)
(16)\(\Large \frac{h}{2 n} \normalsize\) (17)\(u_{2} - 2 u_1 +u_{0}\) (18)\(y_0 + i \times \Delta y\)