メニューに戻る

05:45 にページが自動更新されます。

乱流とそのモデリング

学籍番号
氏　　名
図は乱流の一点における典型的な速度変化を表している．速度変化を次式に示される平均値と変動成分に分けることを考える．
\( u(t) = U + u'(t) \)
\( v(t) = V + v'(t) \)
\( w(t) = W + w'(t) \)
以下の問いに答えなさい．なお，\(\overline{\ \ }\)は\(\Delta T\)間の時間平均を表す．
(A) 平均値\(U\)を定める時間間隔を\( \Delta T\)とすればどのように表せるか？ \(U = \) ()
(B) 単位質量あたりの運動エネルギー\( \frac{1}{2} u^2\)の\( \Delta T\)間の時間平均はどのように表せるか？ \(\displaystyle \frac{1}{\Delta T} \int_{-\Delta T/2}^{\Delta T/2}\frac{1}{2}u^2(t) dt= \) ()
(C) (B)の右辺において\( u'(t)\)を含む項はなんという？ \( \) ()
(D) (C)を\( \frac{1}{2}\overline{u'^2}\)で表し，\(v, w\)についても同様に \( \frac{1}{2}\overline {v'^2}, \frac{1}{2}\overline {w'^2}\)とすれば，
単位質量あたりの乱れの全運動エネルギー\(k\)は\(\frac{1}{2}(\overline {u'^2}+\overline {v'^2}+\overline {w'^2})\)となる．
乱流強度が\(\displaystyle T_i = \sqrt{\frac{\overline {u'^2}+\overline {v'^2}+\overline {w'^2}}{U^2+V^2+W^2}}\)で定義され，
\(\displaystyle U_{ref}=\sqrt{\frac{U^2+V^2+W^2}{3}} \)とすれば，
\( T_i \)は\( k \)と\( U_{ref} \)を用いどのように表せるか？
 \(T_i = \) ()
【補　足】
\( \overline{u} = \overline{U+u'} = \overline{U} + \overline{u'} = U\)
平　　均： \( \displaystyle \bar{a} = \frac{1}{T} \int_{0}^{T} a(t) dt\)
分　　散： \( \displaystyle \frac{1}{T} \int_{0}^{T} \{a(t)-\bar{a}\}^2 dt\)
標準偏差： \( \displaystyle \sqrt{\frac{1}{T} \int_{0}^{T} \{a(t)-\bar{a}\}^2 dt}\)

乱流の一点における典型的な速度変化（定常流れ）

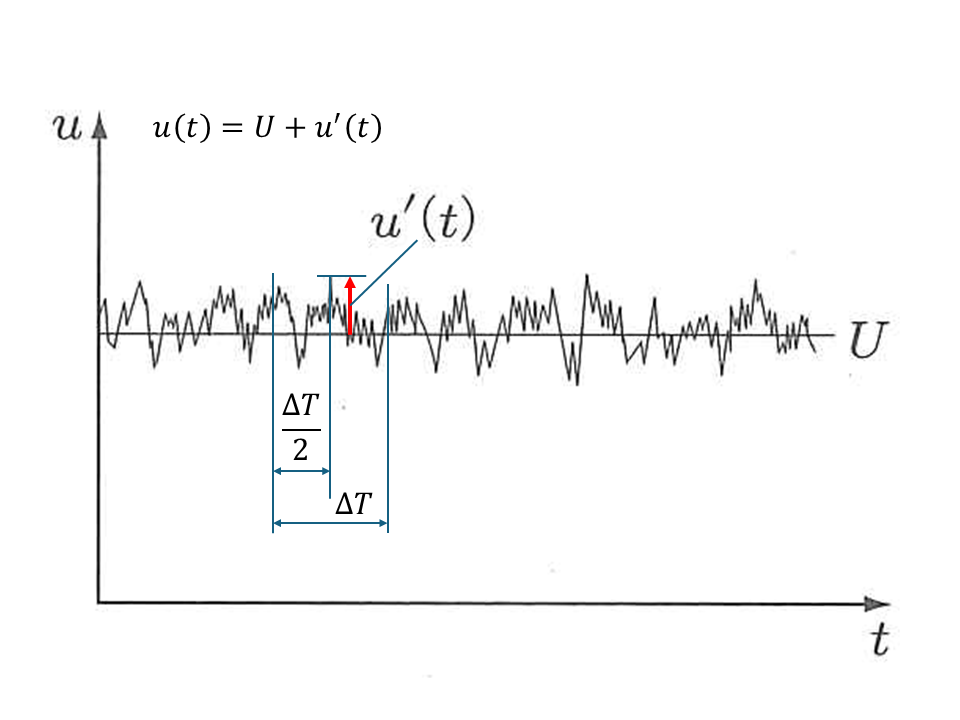
図0014 乱流の一点における典型的な速度変化（定常流れ）



選択肢

【定期試験に出題される場合，解答は選択肢】
(1)\(位置エネルギー\) (2)\(\displaystyle \frac{1}{\Delta T} \int_{-\Delta T/2}^{\Delta T/2} u'(t) dt \) (3)\(\displaystyle \frac{k^{1/2}}{U_{ref}}\)
(4)\(\displaystyle \frac{1}{\Delta T} \int_{-\Delta T/2}^{\Delta T/2} \frac{1}{2}u'^2(t) dt \) (5)\(\displaystyle \frac{1}{2} U^2\) (6)\(乱流エネルギー\)
(7)\(\displaystyle \frac{(2k)^{1/2}}{U_{ref}}\) (8)\(\displaystyle \frac{(\frac{1}{3}k)^{1/2}}{U_{ref}}\) (9)\(\displaystyle \frac{1}{\Delta T} \int_{-\Delta T/2}^{\Delta T/2} u(t) dt \)
(10)\(内部エネルギー\) (11)\(\displaystyle \frac{1}{2} U^2 + \frac{1}{\Delta T}\int_{-\Delta T/2}^{\Delta T/2} \frac{1}{2}u'^2(t) dt \) (12)\(\displaystyle \frac{(\frac{2}{3}k)^{1/2}}{U_{ref}}\)