メニューに戻る

05:44 にページが自動更新されます。

乱流とそのモデリング

学籍番号
氏　　名
図は乱流の一点における典型的な速度変化を表している．体積力を無視したNS方程式においてx方向の時間平均を考える．
\( u(t,x,y,z) = U(t,x,y,z) + u'(t,x,y,z) \)
\( v(t,x,y,z) = V(t,x,y,z) + v'(t,x,y,z) \)
\( w(t,x,y,z) = W(t,x,y,z) + w'(t,x,y,z) \)
\( p(t,x,y,z) = P(t,x,y,z) + p'(t,x,y,z) \)
\(\vec{u}=(u,v,w)\)
\(\vec{U}=(U,V,W)\)
\(\vec{u'}=(u',v',w')\)
NS方程式（x方向成分）： \(\displaystyle \frac{\partial u}{\partial t} + \text{div} (u \vec{u}) = -\frac{1}{\rho}\frac{\partial p}{\partial x} + \nu\ \text{div}(\text{grad}\ u)\)
\(\displaystyle \overline{\frac{\partial u}{\partial t} + \text{div} (u \vec{u})} = \overline{-\frac{1}{\rho}\frac{\partial p}{\partial x} + \nu\ \text{div}(\text{grad}\ u)} \)
以下の問いに答えなさい．なお，\(\overline{\ \ }\)は\(\Delta T\)間の時間平均を表す．（微分と積分の順序は交換可能）
(A) 平均値\(U\)を定める時間間隔を\( \Delta T\)とすればどのように表せるか？ \(U(t) = \) ()
(B) 単位質量あたりの運動エネルギー\(\displaystyle \frac{1}{2} u^2\)の\( \Delta T\)間の時間平均はどのように表せるか？ \(\displaystyle \frac{1}{\Delta T} \int_{-\Delta T/2}^{\Delta T/2}\frac{1}{2}u^2 dt= \) ()
(C) \(\displaystyle \frac{\partial u}{\partial t}\)の時間平均はどのように表せるか？ \(\displaystyle \overline{\frac{\partial u}{\partial t}} = \) ()
(D) \(\displaystyle \text{div} (u \vec{u})\)の時間平均はどのように表せるか？ \(\overline{\text{div} (u \vec{u})} = \) ()
(E) \(\displaystyle {-\frac{1}{\rho}\frac{\partial p}{\partial x}}\)の時間平均はどのように表せるか？ \(\displaystyle \overline{-\frac{1}{\rho}\frac{\partial p}{\partial x}} = \) ()
(F) \(\displaystyle {\nu\ \text{div}(\text{grad}\ u)}\)の時間平均はどのように表せるか？ \(\displaystyle \overline{\nu\ \text{div}(\text{grad}\ u)} = \) ()
(G) 体積力を無視したNS方程式の時間平均はどのように表せるか？ \(\displaystyle \frac{\partial U}{\partial t} + \text{div} (U \vec{U}) = -\frac{1}{\rho}\frac{\partial P}{\partial x} + \nu\ \text{div}(\text{grad}\ U) + \) ()
\(\displaystyle \text{div}(u'\vec{u'}) = -\frac{1}{\rho}\text{div}(-\rho u' \vec{u'}) \)
レイノルズ応力：\(-\rho u' \vec{u'} \)のモデリング \(\rightarrow \mu_t \ \text{grad}\ U \)
\( \mu_t \propto \Large \frac{k^2}{\epsilon}\)：\(k\)：乱流エネルギー, \(\epsilon\)：散逸率（\(k\)が熱に変わる[損失]割合）で，それぞれ輸送方程式を構築【\( k- \epsilon\)モデル】
乱流の一点における典型的な速度変化（非定常流れ）

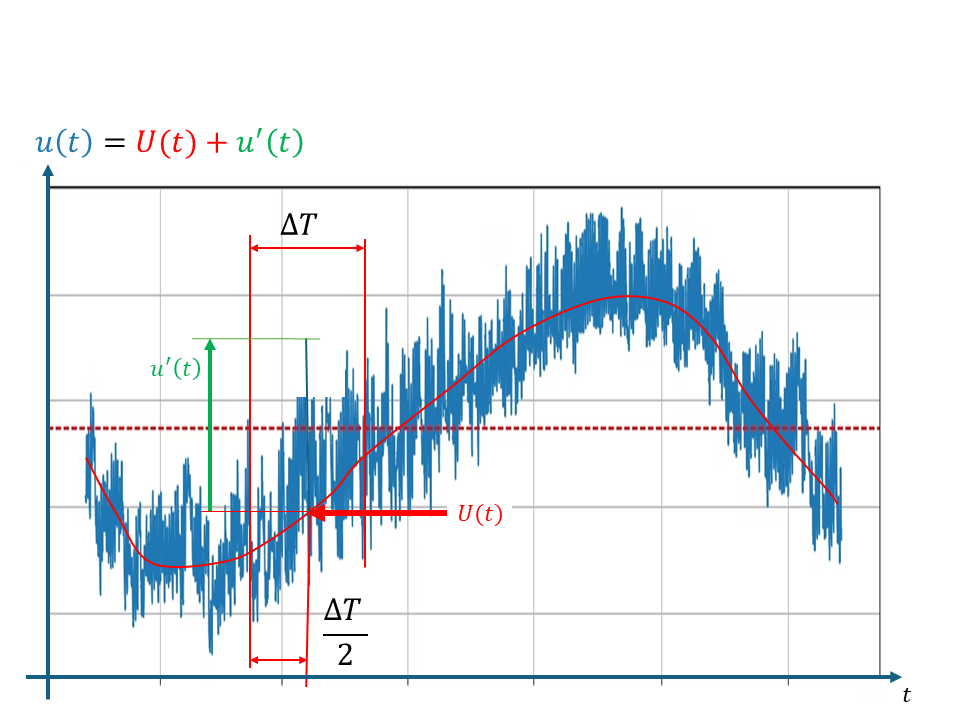
図0015 乱流の一点における典型的な速度変化（非定常流れ）

選択肢

【定期試験に出題される場合，解答は選択肢】
(1)\(\displaystyle \text{div} (\overline{u' \vec{u'}})\) (2)\(\displaystyle \frac{\partial u'}{\partial t}\) (3)\(\displaystyle \frac{1}{2} U^2\)
(4)\(\displaystyle \nu\ \text{div}(\text{grad}\ U)\) (5)\(\displaystyle \frac{1}{\Delta T} \int_{-\Delta T/2}^{\Delta T/2} \frac{1}{2}u'^2 dt \) (6)\(\displaystyle \text{div} (U \vec{U}) + \text{div} (\overline{u' \vec{u'}})\)
(7)\(\displaystyle \frac{1}{\Delta T} \int_{-\Delta T/2}^{\Delta T/2} u dt \) (8)\(\displaystyle -\frac{1}{\rho}\frac{\partial P}{\partial x}\) (9)\(\displaystyle \frac{\partial u}{\partial t}\)
(10)\(\displaystyle \frac{1}{2} U^2 + \frac{1}{\Delta T}\int_{-\Delta T/2}^{\Delta T/2} \frac{1}{2}u'^2 dt \) (11)\(\displaystyle \frac{1}{\rho}\text{div}(\rho\ \overline{u'\vec{u'}})\) (12)\(\displaystyle \frac{\partial U}{\partial t}\)
(13)\(\displaystyle \text{div} (U \vec{U})\) (14)\(\displaystyle \frac{1}{\Delta T} \int_{-\Delta T/2}^{\Delta T/2} u' dt \) (15)\(\displaystyle \frac{1}{\rho}\text{div}(-\rho\ \overline{u'\vec{u'}})\)
【補　足】
\(\displaystyle \overline{\vec{u}} = (\overline{u},\overline{v},\overline{w})\)
\(\displaystyle \overline{u\vec{u}} = (\overline{uu},\overline{uv},\overline{uw})\)
\(\displaystyle \overline{uv} = \overline{(U+u')(V+v')} = UV + \overline{u'v'} + U\overline{v'} + V\overline{u'} = UV + \overline{u'v'} \)
\(\displaystyle \text{grad}\ A = (\frac{\partial A}{\partial x},\frac{\partial A}{\partial y},\frac{\partial A}{\partial z})\)
\(\displaystyle \text{div}(\vec{A}) = \frac{\partial Ax}{\partial x} + \frac{\partial Ay}{\partial y} + \frac{\partial Az}{\partial z}\)
（微分と積分の順序は交換可能）
\(\displaystyle \overline{\text{grad}\ A} = \text{grad}\ \overline{A} \)
\(\displaystyle \overline{\text{div}(\vec{A})} = \text{div}(\overline{\vec{A}}) \)