メニューに戻る

１時間後にページが自動更新されます。

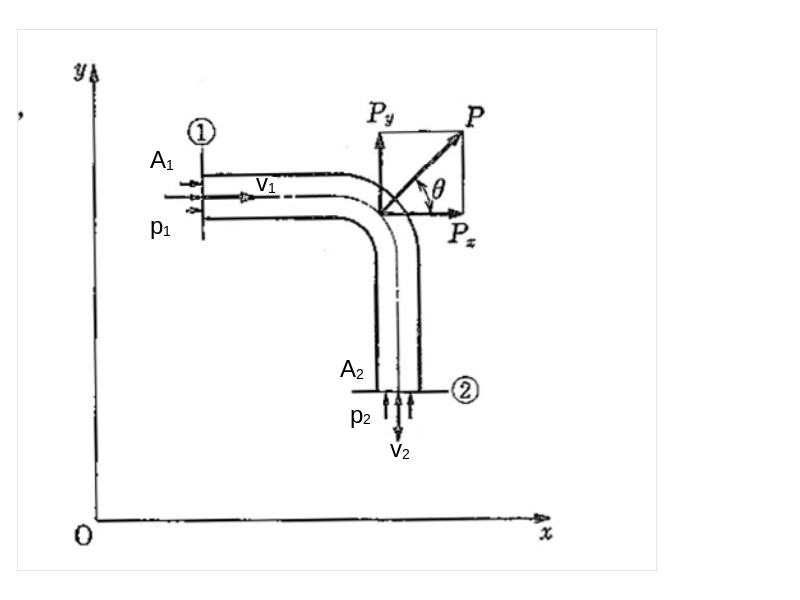
運動量保存則
テキスト例題４．４と同類の問題

学籍番号
氏　　名
下図のように入口直径 \( \phi D_1 \) ,出口直径 \( \phi D_2 \) の 90°の曲管が水平に設置され（基準面からの高さ \( h \)）,その中を水（密度\( \rho \)）が流量 \( Q \) で流れている．
曲管の入口の平均圧力を \( p_1 \) とするとき,この曲管に及ぼす水の力の大きさと方向を次の手順にしたがって求めなさい．
ただし,曲管内の摩擦などによる損失は無視する．
なお,\( \bigcirc \!\!\!\!\!{1}\, \)流入断面積 \( A_1 \), \( \bigcirc \!\!\!\!\!{2}\, \)流出断面積 \( A_2 \),重力加速度は \( g \) で表す．
(1) 流入断面および流出断面における平均速度は \( v_1 \,=\, \)(),\( v_2 \,=\, \)() である．

運動量・力（\( \bigcirc \!\!\!\!\!{1}\, \)から\( \bigcirc \!\!\!\!\!{2}\, \)間の流体）大きさx方向成分y方向成分
\( \bigcirc \!\!\!\!\!{1}\, \)断面を通過する運動量(A) = ()(A)×()(A)×()
\( \bigcirc \!\!\!\!\!{2}\, \)断面を通過する運動量(B) = ()(B)×()(B)×()
\( \bigcirc \!\!\!\!\!{1}\, \)断面の流体に働く圧力の力 (C) = ()(C)×()(C)×()
\( \bigcirc \!\!\!\!\!{2}\, \)断面の流体に働く圧力の力 (D) = ()(D)×()(D)×()
\( \bigcirc \!\!\!\!\!{1}\, \)\( \bigcirc \!\!\!\!\!{2}\, \)間の流体が壁面から受ける力PPxPy
\( \bigcirc \!\!\!\!\!{1}\, \)\( \bigcirc \!\!\!\!\!{2}\, \)間の壁面が流体から受ける力D = ()Dx = ()Dy = ()

断面を毎秒通過する運動量の大きさ：（ 質量流量 ）×（ 流速 ）：\( [N] = [(kg/s) \cdot (m/s)] \)
　運動量は力と同様にベクトルであり，大きさと方向をもつ．

作用と反作用の関係：大きさは等しく向きは逆
たとえば，\( (D_x, D_y) = (10,10) \) であれば \( (P_x, P_y) = (-10,-10) \)


運動量保存則断面 \( \bigcirc \!\!\!\!\!{1}\, \)\( \bigcirc \!\!\!\!\!{2}\, \) を毎秒通過する運動量の変化 \(=\)
（流出断面\( \bigcirc \!\!\!\!\!{2}\, \) から流入断面 \( \bigcirc \!\!\!\!\!{1}\, \)の運動量を引く）		\( \bigcirc \!\!\!\!\!{1}\, \)\( \bigcirc \!\!\!\!\!{2}\, \)間の流体に働く力
x方向()×() \( - \) ()×() \( = \) Px \(+\) ()×\( p_1 A_1 \) \(+\) ()×\( p_2 A_2 \)
y方向()×() \( - \) ()×() \( = \) Py \(+\) ()×\( p_1 A_1 \) \(+\) ()×\( p_2 A_2 \)

\( A \,=\, A_1\,=\, A_2 \) の場合, 断面 \( \bigcirc \!\!\!\!\!{1}\, \)，\( \bigcirc \!\!\!\!\!{2}\, \) における圧力と速度は、
\[ Q \,=\, A_1 v_1 \,=\, A_2 v_2 \]より，\( v_1 = v_2 \) \[ \frac{p_1}{\rho }+\frac{v_1^2}{2}+gh = \frac{p_2}{\rho }+\frac{v_2^2}{2}+gh \] より，\( p_1 = p_2 \)となるので，\( \, p , v \) と表せば,
Dx = ()\(+\)()
Dy = ()\(+\)()


選択肢

(1)\(\Large 1\) (2)\(\Large -p A\) (3)\(\Large \rho Q v\) (4)\(\Large -P_y\) (5)\(\Large \rho Q v_2\) (6)\(\Large -\rho Q v\)
(7)\(\Large \frac{Q}{A_2}\) (8)\(\Large p A\) (9)\(\Large P_x\) (10)\(\Large P_y\) (11)\(\Large p_1 A_1\) (12)\(\Large P\)
(13)\(\Large -P_x\) (14)\(\Large p_2 A_2\) (15)\(\Large \frac{Q}{A_1}\) (16)\(\Large -1\) (17)\(\Large 0\) (18)\(\Large \rho Q v_1\)