メニューに戻る

03:13 にページが自動更新されます。

摩擦速度と管摩擦係数

学籍番号
氏　　名
一様速度\(U\)の流れに置かれた平板上に発達する層流境界層の速度分布\( u(x, y) \)は，平板先端からの距離\( x\)に対し相似であり，
壁面からの高さ\(y\)を境界層の厚み\(\delta(x)\)で無次元化する高さを\(\eta = \Large \frac{y}{\delta(x)} \normalsize\)とすると，
\( \Large \frac{u(\eta)}{U} \normalsize = 2 \eta -\eta ^2\) で表せる．以下の手順に従って\(\delta(x)\)を求めなさい．
(A) 運動量厚さ\( \theta \)と壁面せん断応力\( \tau_w \)の関係は？ \(\tau_w =\) ()
(B) 速度分布\(u(\eta)\)の１階微分は？ \(\Large \frac{du}{d\eta} =\) ()
(C) \(\eta(y)\)の１階微分は？ \(\Large \frac{d\eta}{dy} =\) ()
(D) 速度分布\(u(\eta)\)とせん断応力\( \tau \)の関係は？ \(\tau =\) ()
(E) 速度分布\(u(\eta)\)と\( \eta=0(y=0)\)におけるせん断応力（壁面せん断応力）\( \tau_w \)の関係は？ \(\tau_w =\) ()
(F) 運動量厚さ\( \theta \)を速度分布\(u(\eta)\)から求めれば？ \(\theta =\) ()
(G) (A)～(F)をまとめ,\(\delta(x)\)の微分方程式を導くと？ \(\Large \frac{d \delta}{dx} =\) ()
(H) 平板雄先端（\( x=0\)）における境界層の厚みを\( \delta = 0\)として(G)を解くと？ \(\delta =\) ()

粘性係数（粘度）\( \mu \)と密度(\( \rho \))の比は動粘性係数（動粘度）\( \nu\)で表すことがおおい．\(\displaystyle \frac{\mu}{\rho} = \nu\)



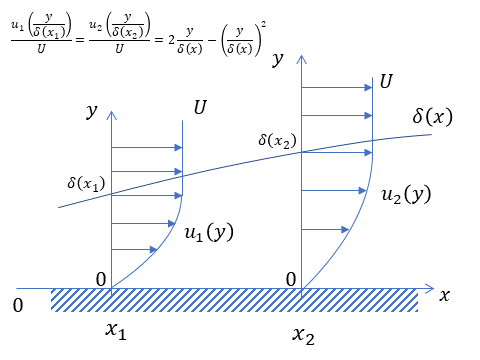
選択肢

(1)\(2U (1 - \eta)\) (2)\(\Large \frac{15 \mu}{\rho U} \) (3)\(\rho U^2 \Large \frac{d \theta}{dx} \normalsize \) (4)\(\sqrt{\Large \frac{30 \mu x}{\rho U}} \)
(5)\(\sqrt{\Large \frac{15 \mu x}{\rho U}} \) (6)\(\delta\) (7)\(\mu \Large \frac{du}{d \eta} \frac{d \eta}{dy}\normalsize \) (8)\(\Large \frac{1}{15} \normalsize \delta \)
(9)\(\Large \frac{30 \mu}{\rho U} \) (10)\(\Large \frac{2 \mu U}{\delta} \) (11)\(\Large \frac{2}{15} \normalsize \delta \) (12)\(\Large \frac{1}{\delta}\)
(13)\(2 \mu U \delta \)